Sludge separation − centrifugation

Posted on 22 June 2020

Circles/uneven strata of different blues from light blue/yellow on the outside to dark blue/black at the centre

Overview of sludge centrifugation

The theory of centrifugation relates to sedimentation theory, since centrifugation acts to enhance gravity through the centrifugal force (or G force). The migration velocity of an unhindered spherical particle of diameter d under the influence of a centrifugal force is given by:

\begin{equation} v_s=\frac{\left(\omega^2r\left(\rho_s-\rho\right)d^2\right)}{18\mu} \end{equation}

where:

ω is the angular velocity in radians/s (where frequency (Hz) = 2πω)

r is the radius of rotation in m,

μ is the dynamic viscosity in kg/(m.s), and

ρ_s and ρ are the respective densities of the particle and water in kg/m³.

This is the same as the Stokes Law equation from sedimentation theory, with ω²r replacing the gravitational constant g.

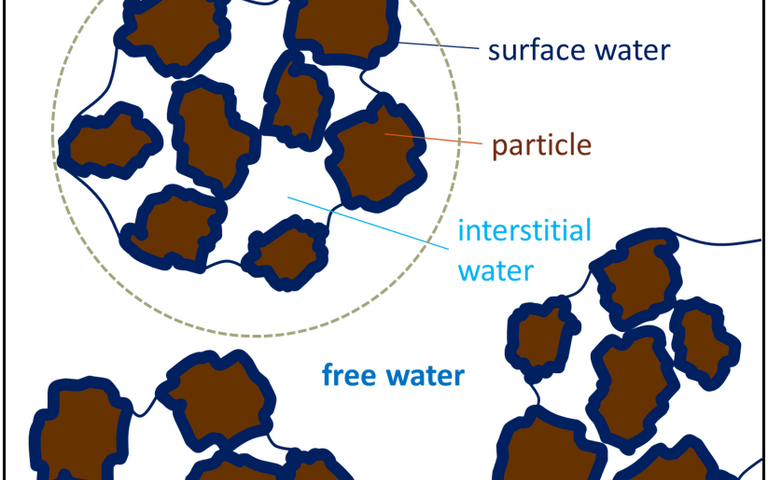
As with sedimentation theory, this equation is a simplification. In practice, particles are not spherical, and do not migrate in isolation but interact with others around it migrating at the same time (i.e., they are hindered). A number of correction factors are applied to account for these effects to provide the effective volumetric throughput Q of the centrifuge in m³/s:

| sponsored

\begin{equation} Q=\frac{\left(\omega^2r\left(\rho_s-\rho\right)d^2VF_p\right)}{18\mu\theta D} \end{equation}

where

V is the centrifuge internal volume,

F_p is a factor correcting for hindered migration, decreasing with increasing solids concentration,

θ is a shape factor (equalling 1 for spherical particles and increasing with decreasing sphericity), and

D is the distance the particle migrates before being retained in the centrifuge.

F_s roughly equals 1, 0.5, 0.1 and 0.05 for solids volume fractions of 1%, 3%, 12% and 20% respectively. The efficiency of solids removal depends on the residence time within the centrifuge, equal to Q/V, and the migration distance D. The maximum D value is given by the annular gap, equal to the difference in radius between the rotary screw and the inner surface of the bowl.

The centrifugation process efficiency is therefore dependent on the solids volume fraction, since this impacts on F_s, the effective surface area (A = V/D), and the force provided by the angular rotation velocity ω and the radius r, ω²r. The force is usually normalised against the acceleration due to gravity g (9.81 m/s²) to give ω²r/g – the unitless G force (G).

The product of the G force and the effective surface area, GA = ω²rV/(gD), is referred to as the sigma factor ∑, taking units of m². ∑ represents the cross-sectional area of a gravity thickener having the same capacity.